6. Kreise und ihre Schnittmenge
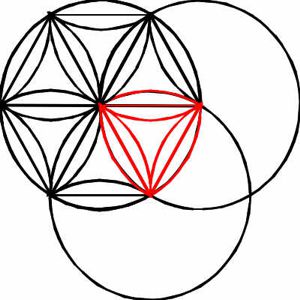
Zeichnerische Lösung:
Wie auf dem Bild zu sehen, enthält die Schnittfläche drei "Zigarren" und einen konkaven Dreiseiter.
Der gesamte Kreis enthält insgesamt zwölf Zigarren und sechs Dreiseiter.
Die Schnittfläche muss also kleiner als ein Viertel des Kreises sein!
Rechnerische Lösung:
Berechne zunächst mithilfe von Pythagoras die Höhe und damit die Fläche des gleichseitigen Dreiecks, dessen Ecken die Mittelpunkte der Kreise bilden.
Diese Fläche ist gleich Wurzel(3) * r² / 4.
Dieses Dreieck plus ein Bogensegment bildet einen Kreisausschnitt mit dem Winkel von 60 Grad.
Die Fläche dieses Kreisausschnitts ist gleich PI * r² / 6
Die Gesamtfläche der Schnittfläche ist gleich drei Kreisausschnitte minus 2 Dreiecke.
Durch entsprechendes Umformen erhält man: A = (PI - Wurzel(3)) * r² / 2
Bei einem Kreisradius von 1 ergibt sich so 0,7047709 als Schnittfläche, während die Kreisfläche
natürlich 3,1415927 beträgt. Die Schnittfläche ist somit kleiner als ein Viertel eines Kreises!

